5.4 Row-echelon reduction

The preceding example of Gaussian made use of row operations but skipped over the details of how those operations were selected. At this point, it should be noted that no one except a student of an introductory Linear Algebra class actually does Gaussian elimination by hand. There are many computer programs and program libraries designed to do this sort of thing. However, doing it by hand is a significant learning tool and should not be bypassed lightly. It requires many individual calculations of the sort better characterized as arithmetic than mathematics and prone to errors.

For the less numerate among us who wish to check their work for accuracy, Myron provides a convenient way to perform row-echelon reduction on a row-operations by row-operation basis. Start by applying the Gauss helper ^[1] to a matrix. This annotates the matrix with an interactive aide called the Gauss helper:

In the Gauss helper, the matrix is decorated with a column of row-selector buttons. To the right is a row of action buttons and below them an expression template with a Go button. As shown, the initial expression is invalid, with negative row indices and a default operator. The general technique is to select rows, then an action, then apply a generated expression by touching Go . Each time an action button is applied, the expression is changed. Each time an expression is applied, the matrix is changed. The expressions conform to the Gaussian operations listed above.

For the matrix in question, the first row has zeroes in the first two columns, so it should be exchanged with the third row. To do this, touch 0 , then 2 , then ⇄ . The display changes to

After touching on Go , the display changes to

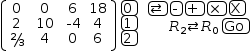
Now the first row should be changed so the leading non-zero element is 1. To do this, multiply the row by 3/2. In the Gauss helper, select 0 , then × . The display changes to

and application of the Go button changes the first row so the matrix is [(1, 6, 0, 9), (2, 10, -4, 4), (0, 0, 6, 18)].

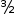
To set the first element of row 1 to 0, subtract twice row 0 from row1. In the helper, touch on 0 , then 1 then - to achieve

Application of Go produces [(1, 6, 0, 9), (0, -2, -4, -14), (0, 0, 6, 18)]. Now multiply row 1 by -(1/2) and row 2 by 1/6. The final result is [(1, 6, 0, 9), (0, 1, 2, 7), (0, 0, 1, 3)].

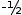
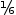
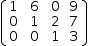
Note the following.

• Selecting an action from the action row does not apply that action; it merely helps to prepare the expression to be executed. Execution occurs when the Go button is applied.
• When two rows are involved, the last row selected is the target.
• The constant depends on the action.
  • If the action is × , the constant is the reciprocal of the leading non-zero element in the row.
  • If the action is - , the constant depends on the order of the row operands.
    • If the destination row is below the source row, the constant is the leading non-zero element of the destination row divided by the corresponding element in the source row.
    • If the destination row is above the source row, the constant is the multiple of the leading non-zero element of the destination row divided by the corresponding element in the source row.
  • If the action is + , the constant is the inverse of the constant generated for - .
• Rows and actions can be selected in any order. The form of the expression is recreated after each selection.

The intent of the somewhat Byzantine constant selection rules is to help in inverting a matrix. For now, as long as the destination row is below the source row, and as long as its leading element is not to the left of the leading element of the source row, application of the - action will reduce the leading element to 0.